Del/nabla operators are used as differentiation operators and are used to find derivatives of function in higher dimensions.
Definition: 𝛻 is defined in terms of partial derivative with pⁿ where n denotes the number of dimensions (Ex- p² ≡ (xy, yz, zx) and basis {e₁, e₂, ..., en} (set of vectors whose components are zero except one)-
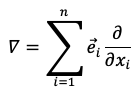
Important Points:
Del is a vector differential operator.
Derivative and gradient though perform the same operation, but there lies a difference in the input-
Derivatives are yielded when- 𝛻 is applied to one independent variable function.
Gradient is the result when the input or del operator is used in the case of a multidimensional scalar function.
Now we will deal with the special operators basically the usage of the Del operator.
Del operator is used for simplification of functions with gradient, curl, divergence, etc.
Gradient
Vector differentiation of scalar field (two observers using the same units will have the same magnitude in spacetime regardless /independent of their position) is called gradient.
Divergence
Divergence is a measure of the tendency of a vector field to converge towards or diverge from a point.
Divergence of a vector space results in a scalar field represented by-
Curl
The density of circulation at each point of the vector field is called the curl operator.
A curl of a vector field P at a point k along the projected vector ň is
Where the integration is calculated in a space of boundary B with S being the area of the field and the magnitude of area.
Laplacian Operator
Divergence of the gradient of scalar function gives a differential operator -Laplacian Operator.
Some Corollaries
To understand and comprehend this we need to know just the basic concepts of scalar and vector products.
Here just for convenience we once again define 3 operators-
𝛻 x 𝛻𝑓 = 0 - Curl of gradient always equal to zero-Here comes the concept of the Irrotational vector Field.
𝛻 ⋅ 𝛻 x 𝐹 = 0 - Divergence of curl always equal to 0. Here comes the concept of the incompressible vector field.
So, this minimum knowledge of the Del operator is enough to understand the mathematical analysis in some parts of this book.