Most of us know about Trigonometry- which works with the relation of angle and sides. Now we shall move to a fundamental concept-quite helpful in solving problems of astronomy and astrophysics.
But before moving into the main topic we must know about Great Circles.
Great Circles
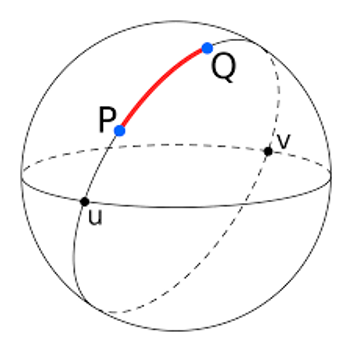
Definition: If a circle is plotted/drawn on a sphere such that the radius of the drawn circle is equal to the radius of the sphere is called a Great Circle.
Important Points
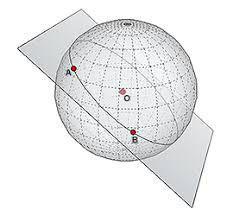
Any other circle drawn on the sphere such that the radius of the circle is not equal to the radius of the sphere then it is a small circle.
The intersection of a sphere with a plane is a circle.
SPHERICAL TRIANGLE
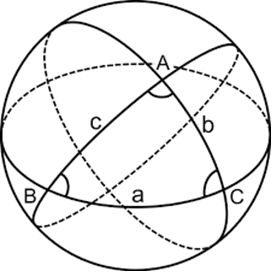
A figure formed by arcs of Great Circles that pass by 3 points connected by pairs.
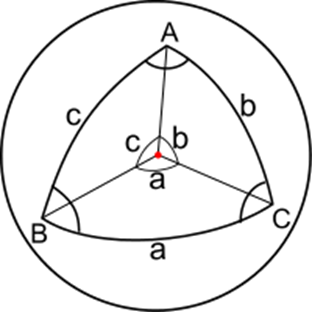
Here A, B, and C are the lengths of the sides and a, b, and c are their corresponding angles of the spherical triangle.
The sum of the angles of a spherical triangle is always greater than 180°.
Spherical Excess (E):
E = A + B + C - 180°. It is not a constant but depends on the triangle.
The area of a spherical triangle is A = ER² where R is the radius of the sphere.
SPHERICAL LAW OF SINES
The spherical law of sines states that
sin a sin b sin c
_____ = _____ = _____
sin A sin B sin C
SPHERICAL LAW OF COSINES
The spherical law of cosines states that
cos c = cos a cos b + sin a sin b sin c